\( \documentclass[12pt]{article} \geometry[margins= 1in]{letterpaper} \)

Section 1 Introduction

A tensor is a multidimensional array, where the order of tensor denotes the dimension of the array. For example, a scalar is simply an order-0 tensor, a vector order-1, a matrix order-2, and any tensor with order-3 or greater is described as a higher order tensor. For this paper I will be focusing on the simplest higher-order tensor, the order-3 tensor, which can be visualized as a sort of Rubik's cube.

In discussing higher order tensors there is some fundamental language that must first be understood. Analogous to rows or columns of a matrix, 3rd-order tensors have fibers. Since there are 3 dimensions to a 3rd-order tensor there are 3 types of fibers generated by holding two of the indexes constant. These fibers are named similarly to the vector elements of a matrix. There are row, column, and tube fibers, which are visualized in Figure 2.1 from Kolda and Bader (2009)[3]. In addition to fibers, 3rd-order tensors also have slices generated by holding one of the indexes constant. The slices resemble matrices that, when stacked together, form a tensor. A 3rd-order tensor can be sliced in 3 directions producing horizontal, lateral, and frontal slices which are visualized in Figure 2.2 from Kolda and Bader (2009)[3].
Figure 1: Adapted from Kolda and Bader (2009)[3]
In quantum chemistry 3rd-order tensors arise naturally as the the outer product of a matrix and a vector, which occurs when calculating spectroscopic properties [2]. In dealing with 3rd-order tensors it is difficult to expand on standard matrix manipulations such as rotation by multiplication with a rotational matrix. To perform these manipulations on higher-order tensors the tensor has to be decomposed into vector or matrix components that can be manipulated and then used to reform a new, rotated tensor. This can be accomplished by performing a CANDECOMP/PARAFAC (CP) decomposition. This process is a nontrivial task and commonly utilizes an alternating least squares (ALS) method [4]. While the ALS method is relatively easy to implement as an expanded version of the standard least squares method, it does not always converge on a solution causing computational difficulties [3]. For this reason many more computational methods have been developed for dealing with special cases involving 3rd-order tensors. In this paper, I lay out some of the common properties of third order tensors, discuss Higher Order SVD and CP decompositions, and how these apply to problems in quantum chemistry.

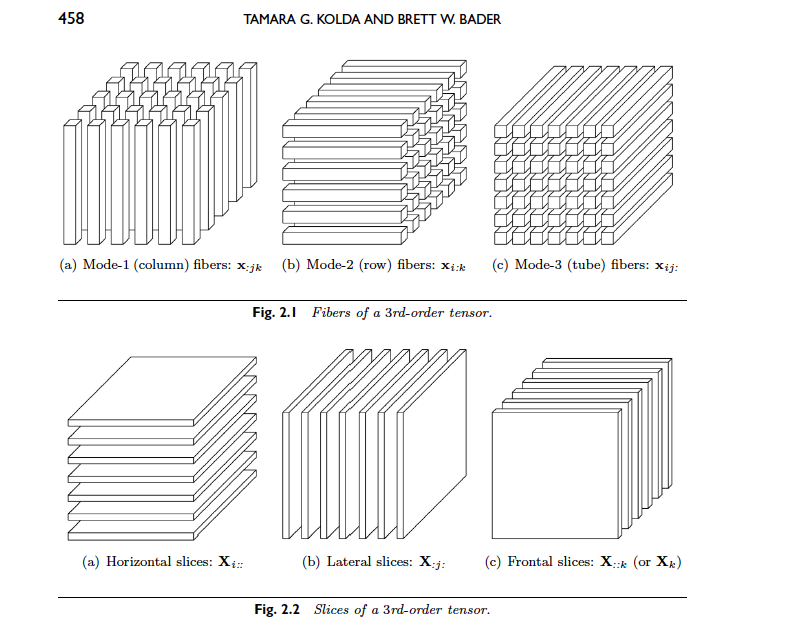
Section 2 3rd-Order Tensor Decompositions

Subsection 2.1 Modal Operations

To discuss the Higher Order SVD, we must first have a general understanding of two modal operations, modal unfoldings and modal products.

For a 3rd-order tensor, \(\mathcal{A} \in \mathbb{R}^{n_1 \times n_2 \times n_3}\), there are 3 modal unfoldings and in general a \(d\)-order tensor has \(d\) modal unfoldings. As a simple example the modal unfoldings for \(\mathcal{A} \in \mathbb{R}^{3 \times 4 \times 2}\) are shown below, where \(\mathcal{A}_1\) and \(\mathcal{A}_2\) are the frontal slices of \(\mathcal{A}\). \[\mathcal{A}_1 = \begin{bmatrix} 1 & 2 & 3 & 4\\ 5 & 6 & 7 & 8\\ 9 & 10 & 11 & 12 \end{bmatrix} \quad \mathcal{A}_2 = \begin{bmatrix} 13 & 14 & 15 & 16\\ 17 & 18 & 19 & 20\\ 21 & 22 & 23 & 24 \end{bmatrix} \] \[\mathcal{A}_{(1)} = \begin{bmatrix} 1 & 2 & 3 & 4 & 13 & 14 & 15 & 16\\ 5 & 6 & 7 & 8 & 17 & 18 & 19 & 20\\ 9 & 10 & 11 & 12 & 21 & 22 & 23 & 24 \end{bmatrix}\] \[\mathcal{A}_{(2)} = \begin{bmatrix} 1 & 5 & 9 & 13 & 17 & 21\\ 2 & 6 & 10 & 14 & 18 & 22\\ 3 & 7 & 11 & 15 & 19 & 23\\ 4 & 8 & 12 & 16 & 20 & 24 & \end{bmatrix}\] \[\mathcal{A}_{(3)} = \begin{bmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24 \end{bmatrix}\] Using the definition of modal unfolding we can now define a modal product between a matrix and a tensor. These two operations will be used to generalize the standard SVD definition.

Subsection 2.2 Higher Order SVD (HOSVD)

Informally the Higher Order SVD is simply defined as an SVD for each of the tensors modal unfoldings.

Using this definition, computing an HOSVD for a tensor of order-\(N\) is only as computationally difficult as performing \(N\) matrix SVD's. In practice the SVD of a matrix is useful in compressing a matrix to a representation that is arbitrarily close to the original. Generalizing this to the higher order tensor case can be accomplished by using the unitary matrices \(U_k\) from the HOSVD to find a tensor \(\mathcal{S}\) as follows: (the \(\rightarrow\) is used to denote undoing a modal unfolding) \begin{align} \textbf{U}^{T}_{1} \mathcal{A}_{(1)} &= \hat{\mathcal{A}}_{(1)} \rightarrow \hat{\mathcal{A}}\notag\\ \textbf{U}^{T}_{2} \hat{\mathcal{A}}_{(2)} & = \hat{\hat{\mathcal{A}}}_{(2)} \rightarrow \hat{\hat{\mathcal{A}}}\notag\\ \textbf{U}^{T}_{3} \hat{\hat{\mathcal{A}}}_{(3)} &= \mathcal{S}_{(3)} \rightarrow \mathcal{S}\notag \end{align} This can be denoted by sequential modal products much more concisely. \begin{align} \mathcal{S} &=\mathcal{A}\times_1 U^{T}_{1} \times_2 U^{T}_{2} \times_3 U^{T}_{3}\notag\\ \mathcal{A} &=\mathcal{S}\times_1 U_{1} \times_2 U_{2} \times_3 U_{3}\notag \end{align} This \(\mathcal{S}\) tensor is referred to as the core tensor. While this tensor is not diagonal the entries tend to decrease as distance from the diagonal increases where the diagonal is the entries from the upper left hand corner of the cube to the lower right hand corner. This property is useful when compressing the original \(\mathcal{A}\) because the dimension of \(U\) can be reduced by dropping the smaller terms, and a close approximation will still be generated, much like the compression of a matrix using SVD. The biggest example of this is the compression of color photos where each frontal slice corresponds to intensities of red, green, or blue instead of the matrix example where entries correspond to intensities on the gray-scale. This approach could also be used to first compress a tensor, then perform a CP decomposition on the compressed tensor to save computational resources.

Subsection 2.3 Rank of Higher Order Tensors

The notion of rank with respect to higher order tensors is not as simple as the rank of a matrix.

This definition of rank comes up naturally within many of the common tensor decompositions. For example, in the CANDECOMP/PARAFAC (CP) decomposition the rank specifies the minimum number of vector outer products required to reproduce the tensor exactly. And, with a somewhat circular claim, an exact CP decomposition with minimal vector outer products can be used to determine the rank of a tensor, this is also referred to as a rank decomposition. While the definition for matrix rank is an analog to tensor rank, the properties are quite different. For example, there is no general algorithm to determine the rank of a given higher order tensor. There is only a loose upper bound on the rank of a 3rd-order tensor, \(\mathcal{A}\in\mathbb{R}^{I\times J\times K}\), described by \(rank(\mathcal{A})\leq \mbox{min}\{IJ,IK,JK\}\), but the rank is often lower than this for randomly generated tensors [7].

Subsection 2.4 CANDECOMP/PARAFAC Decomposition

Unfortunately there is no single algorithm to perform a CP decomposition on any tensor. This is partially due to the fact that the rank of a higher order tensor is not known precisely until a CP decomposition has been performed and is known to be the most concise decomposition.

The CP decomposition is nicely visualized by Kolda and Bader (2009) in Figure 3.1.
Figure 1: Adapted from Kolda and Bader (2009)[3]
The vectors of a CP composition, \(a_r\), \(b_r\), and \(c_r\) for \(1 \leq r \leq R\), are often compiled into the columns of the matrices \(\textbf{A}\), \(\textbf{B}\), and \(\textbf{C}\) respectively, and the CP decomposition is written more concisely, \[\mathcal{A}=[[\textbf{A},\textbf{B},\textbf{C}]]\] . This type of matrix multiplication is often denoted by the \(\odot\) symbol. For instance, \[\textbf{A} \odot \textbf{B} = [a_1|a_2|\dots|a_n] \odot [b_1|b_2|\dots|b_n] = [a_1 \circ b_1|a_2 \circ b_2|\dots|a_n \circ b_n]\] The example below, from Bader and Kolda (2009), demonstrates why the rank of a matrix is difficult to determine precisely. In this example a CP decomposition over the real and complex fields is performed for \(\mathcal{A} \in \mathbb{R}^{2 \times 2 \times 2}\) where \(\mathcal{A}_1\) and \(\mathcal{A}_2\) are the frontal slices of \(\mathcal{A}\) [3]. \begin{align} \mathcal{A}_1 &= \begin{bmatrix} 1 & 0\\0 & 1 \end{bmatrix} &\mathcal{A}_2 &= \begin{bmatrix} 0 & 1\\-1 & 0 \end{bmatrix}\notag \end{align} The rank decomposition over \(\mathbb{R}\) is \(\mathcal{A}= [[\textbf{A},\textbf{B},\textbf{C}]]\), where \begin{align} \textbf{A}&=\begin{bmatrix} 1 & 0 & 1\\0 & 1 & -1\end{bmatrix} & \textbf{B}&=\begin{bmatrix} 1 & 0 & 1\\0 & 1 & 1\end{bmatrix} & \textbf{C} &= \begin{bmatrix} 1 & 1 & 0\\-1 & 1 & 1\end{bmatrix}\notag \end{align} but over \(\mathbb{C}\) \begin{align} \textbf{A}&=\frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1\\-i & i \end{bmatrix} & \textbf{B}&=\frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1\\i & -i \end{bmatrix} & \textbf{C}&=\begin{bmatrix} 1 & 1\\i & -i \end{bmatrix}\notag \end{align} This leads to a very surprising property, the rank of a tensor can be different over \(\mathbb{R}\) and \(\mathbb{C}\). For this reason I have restricted the definitions to \(\mathbb{R}\) to remove this ambiguity.

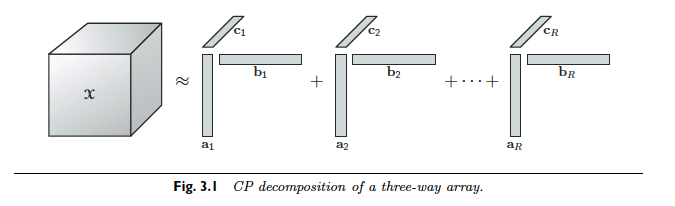
Performing a CP decomposition on a 3rd order tensor \(\mathcal{A}\) is a matter of performing a Alternating Least Squares (ALS) routine to minimize \(||\mathcal{A}_{(1)} - \textbf{A}(\textbf{C}\odot \textbf{B})^T||\). To perform an ALS routine on this system, the system is divided into 3 standard least squares problems where 2 of the 3 matrices are held constant and the third is solved for. The main problem in implementing an ALS routine such as this, is choosing initial values for the two matrices that are held constant to initialize the first least squares problem. This method may take many iterations to converge, the point of convergence is heavily reliant on the initial guess, and the computed solution is not always accurate. Faber, Bro, and Hopke (2003) investigated six methods as an alternative to the ALS method and none of them came out more effective than ALS in terms of accuracy of solution, but some did converge faster [6]. In addition, derivative methods have been developed that are superior to the ALS method in terms of convergence and solution accuracy but are much more computationally expensive [3]. For quantum mechanical problems involving a few \(3 \times 3 \times 3\) tensors accuracy is paramount to computational expense. One such algorithm is the PMF3 algorithm described in Paatero (1997) which computes changes to all three matrices simultaneously. This allows for faster convergence than the ALS method and optional specificity for non-negative solutions reduces divergence in systems that are known to have positive solutions [5].

Section 3 Application to Quantum Chemistry

Subsection 3.1 Introduction of the Problem

In the field of quantum chemistry, linear algebra is heavily utilized and higher order tensors can arise in some specialized problems. In my personal experience, I have encountered 3rd-order tensors while working with the spectroscopic properties of molecules. In practice the issues arise when trying to manipulate 3rd-order tensors, and specifically when trying to rotate a 3rd-order tensor analogous to how a matrix would be rotated for a change in coordinates. For these problems the 3rd-order tensors can arise as an outer product between a matrix and a vector that represent the polarizability and dipole moment, respectively, of a molecule, the outer product of which is the hyperpolarizability tensor. In this case the method used to rotate the hyperpolarizability tensor is to rotate the vector and matrix independently and then recalculating the outer product after each rotation. This method maybe more computationally expensive and could result in numerical inaccuracies after repeated iterations, especially when dealing with small values. This solution is the only one that could be found by my colleagues and me. The true issue arises when the hyperpolarizability tensor is calculated independently by the computational program unless an intuitive user explicitly specifies the separate polarizability and dipole moments, but even then the outer product of the polarizability and dipole moment is only approximately equal to the hyperpolarizability tensor. For this reason it is desirable to have a way to rotate the hyperpolarizability tensor independently.

Subsection 3.2 Rotation Matrices

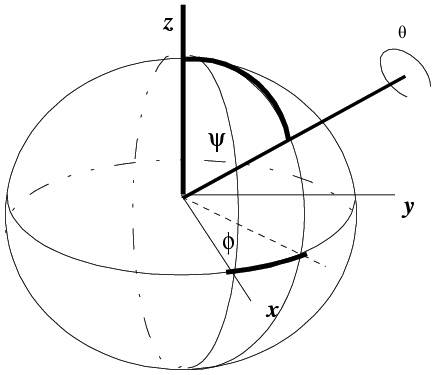
In the context of linear algebra and quantum chemistry, a rotation matrix is a matrix that is used to rotate a set of points in space. In the specific context of spectroscopy, a rotation matrix is used to rotate a molecules properties, such as hyperpolarizability represented by a 3rd-order tensor, about an axis or axes. This process is done to orientationally average molecules over axes that are known to allow free rotation. The rotation matrix commonly used to do this is below and the corresponding axes of rotation are shown in Figure 1 [2], \[R = \begin{bmatrix} \cos (\phi ) \cos (\psi )-\cos (\theta ) \sin (\phi ) \sin (\psi ) & -\cos (\theta ) \cos (\psi ) \sin (\phi )-\cos (\phi ) \sin (\psi ) & \sin (\theta) \sin (\phi ) \\ \cos (\psi ) \sin (\phi )+\cos (\theta ) \cos (\phi ) \sin (\psi ) & \cos (\theta ) \cos (\phi ) \cos (\psi )-\sin (\phi ) \sin (\psi ) & -\cos (\phi ) \sin (\theta ) \\ \sin (\theta ) \sin (\psi ) & \cos (\psi ) \sin (\theta ) & \cos (\theta ) \\ \end{bmatrix}\] It is immediately evident that the rotation matrix gets complex quickly when rotating an object in 3 dimensions around 3 rotational axes. Despite the complexity, this matrix still maintains a very nice property that all rotational matrices have in common, they are unitary. This is significant because it gives us an easy-to-find inverse for an otherwise complex looking matrix and determinant \(1\) guarantees the matrix operated on by the rotation matrix will not be stretched or compressed.

Figure 1: Axes of rotation as described in Wang et al. (2005)[2]

Subsection 3.3 Rotation by CP Decomposition

The most natural solution to this problem after reviewing the decompositions of higher order tensors is to use a CP decomposition. Above it is shown that the CP decomposition produces a sum of vectors, so to rotate a 3rd order tensor we can simply rotate each of the vectors individually by the same angle and then perform the necessary outer products and summations to form the rotated 3rd order tensor. This is mathematically illustrated for the case of \(\mathcal{X} \in \mathbb{R}^{3 \times 3 \times 3}\) where there exists a CP decomposition. In this particular problem we also know that using a value of \(r=3\) will provide an exact decomposition because the tensor should be the outer product of a \( 3 \times 3\) matrix and vector in \(\mathbb{R}^3\) so the resulting tensor should have the same rank as the matrix. Since the matrix is a calculated numerical matrix, its rank is almost certainly 3, thus the tensor rank is 3. Fortunately in this situation, unlike most, the tensor rank is unambiguous so we can write, \[\mathcal{X} = \sum_{j=1}^{3}a_j \circ b_j \circ c_j\] . Then, \begin{align} \mathcal{X}_{Rot} & = \sum_{j=1}^{3} (R a_j) \circ (R b_j) \circ (R c_j)\notag\\ & = [R a_1|R a_2|R a_3] \odot [R b_1|R b_2|R b_3] \odot [R c_1|R c_2|R c_3]\notag\\ & = R[a_1|a_2|a_3] \odot R[b_1|b_2|b_3] \odot R[c_1|c_2|c_3]\notag\\ & = R\textbf{A} \odot R\textbf{B} \odot R\textbf{C}\notag\\ & = [[R\textbf{A},R\textbf{B},R\textbf{C}]]\notag \end{align} This results in only an additional 3 matrix multiplications, which are computationally cheap, but the CP decomposition is computationally expensive. In this case where our 3rd-order tensor is relatively small, the more accurate but more computationally intense PMF3 algorithm can be utilized over the ALS method. This is very beneficial because often in these computations every decimal point is significant and sometimes the number are very small making it more difficult to distinguish between a numerical zero and a significant number. Another thing to keep in mind is that this procedure only applies to a \(3 \times 3 \times 3\) system or a \(2 \times 2 \times 2\) (with a \(2\times 2\) rotational matrix) because rotational matrices have no larger analogs, so the tensors will always be relatively small. However, the decomposition is still nontrivial and is not guaranteed to converge in every situation.

Subsection 3.4 Proposal of a 3rd-Order Rotational Tensor

Disclaimer: This portion is not necessarily mathematically accurate and will be rather conversational.

After spending hours searching, I have been unable to come across a higher order tensor analog to a rotational matrix. In the literature they repeatedly refer to rotating a 3rd-order tensor as, \[\mathcal{X}^{\prime}_{ijk}=R_{li}R_{mj}R_{nk}\mathcal{X}_{lmn}\] but have never been able to find the matrices that behave in this manner plus I would expect that the 3rd-order tensor would have to be rotated by another 3rd-order tensor. For this reason I have been trying to figure out a way to construct a rotational tensor. While working with the CP decomposition and rotation by multiplying each of the vectors with a rotational matrix, I thought what if I did a similar routine multiplying different combinations of the standard unit vectors with a rotational matrix to form the entries of a 3rd-order rotational tensor. \[\mathcal{R}=\sum R e_i \circ R e_j \circ R e_k\] It is often said it is good enough to see what a matrix/linear transformation does on a basis, so if the right basis was used this could be used to form a 3rd-order rotational tensor. In addition, after such a tensor is created, it would be difficult to define it as a rotational tensor because it is hard to translate the concepts like unitary, inverse, and determinant into terms of a higher order tensor.

References

  • G.H. Golub and C.F. Van Loan, Matrix Computations, (The Johns Hopkins University Press 2013).
  • Hongfei Wang et al, 'Quantitative spectral and orientational analysis in surface sum frequency generation vibrational spectroscopy (SFG-VS)', International Reviews in Physical Chemistry (2005), (24) no. 2, 191-256.
  • Kolda, T.G. and Bader, B.W., 'Tensor Decompositions and Applications', SIAM Review (2009), (51) no. 3, 455-500.
  • Carroll, J.Douglas and Chang, Jih-Jie, 'Analysis of individual differences in multidimensional scaling via an n-way generalization of “Eckart-Young” decomposition', Psychometrika (1970), (35) no. 3, 283-319.
  • P. Paatero, 'A weighted non-negative least squares algorithm for three-way ‘PARAFAC’ factor analysis', Chemometrics and Intelligent Laboratory Systems (1997), (38) no. 2, 223-242.
  • N. K. M. Faber and R. Bro, and P. K. Hopke, 'Recent developments in CANDECOMP/PARAFAC algorithms: A critical review', Chemometrics and Intelligent Laboratory Systems (2003), (65), 119-137.
  • J. B. Kruskal, 'Rank, decomposition, and uniqueness for 3-way and N-way arrays, in Multiway Data Analysis', 7-18.