Graph Theory

\( \newcommand{\defint}[4]{\int_{#1}^{#2}\,#3\,d#4} \)

Chapter 3
Gallery

3.1 Introduction

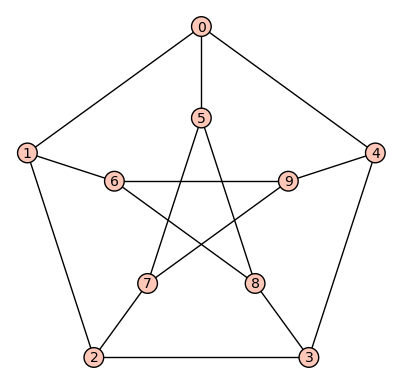
One of the best things about graph theory is that you can draw pictures. Here is a classic.

Figure 3.1: The Petersen graph

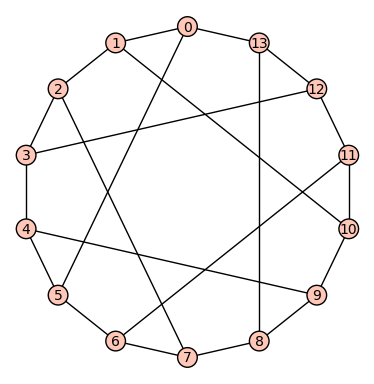
I also like Heawood's graph.

Figure 3.2: The Heawood graph

3.2 Regular Graphs

Regular graphs have a certain amount of combinatorial symmetry.

Definition 3 We call a graph regular if every vertex has the same number of incident edges. This common number is called the degree of the graph.

Figure 3.3: A regular graph

Very pretty, no?

Let's reference a previous definition on walks: Definition 1.

And a reference to the first Heawood graph: Figure 3.2 .

There is a nice proof by induction at this point.